|
3-B/ Les rebonds |
Une collision entraîne forcément la modification du comportement d’un objet.
|
Le rebond sur le segment |
Le rebond de la balle sur la droite Δ d’équation ax + b + cy = 0 se traduit par un changement d’orientation de la vitesse de la balle dans le plan selon les axes x et y.
La balle a une vitesse incidente et une vitesse réfléchie. L’orientation de la droite Δ détermine l’orientation de la vitesse réfléchie.
On peut représenter le rebond avec le schéma ci-dessous :
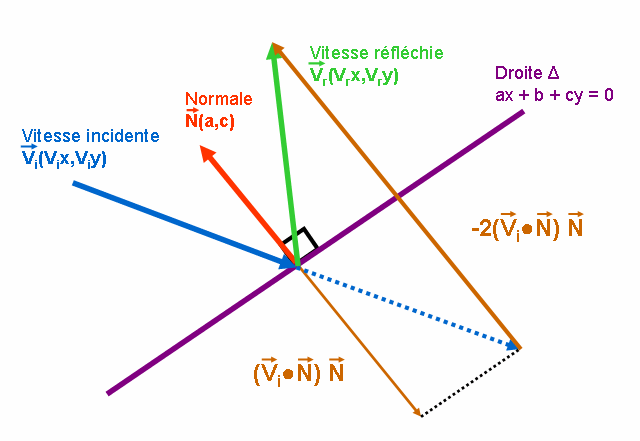
On calcule la vitesse de la balle après rebond à partir de la vitesse incidente de la balle et de la normale au segment de droite.
Les coordonnées de la
normale
à une
droite Δ d’équation ax + b + cy = 0 sont données par les
coefficients a et c, soit
.
Soit
la vitesse
incidente de la balle avant rebond et
la vitesse réfléchie
après rebond.
est le produit
scalaire des vecteurs
et
.
représente la
projection de la vitesse incidente
sur la normale
au segment de
droite.
Par
conséquent : 
C’est-à-dire en développant :
Voilà une capture d’écran montrant le moteur en action. Les lignes noires sont l’ensemble des positions occupées par le centre des deux balles : leur trajectoire. On constate que le centre des balles ne touche jamais les segments percutés.
|
Les exceptions |
1. La balle arrive tangentiellement au segment de droite et percute une des extrémités
Dans ce cas, on considère que la balle doit rebondir sur un segment fictif, perpendiculaire au segment de droite et situé à l’extrémité de ce dernier.
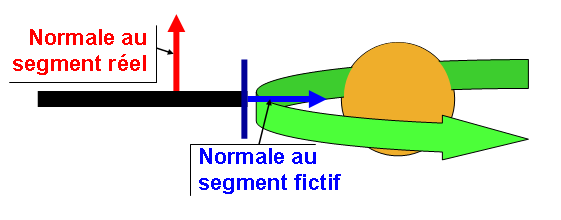
On calcule la vitesse de
la balle après rebond à partir de la vitesse incidente de la balle et de la
normale 
au
segment fictif, qui est perpendiculaire à la normale
au segment de
droite.
avec 
C’est-à-dire en développant :
2. Deux collisions simultanées
Ce cas n’est pas traité par le programme M2D. Il peut être à l’origine d’un disfonctionnement occasionnel. En fait le programme M2D passe en revue toutes les segments de droite et vérifie la présence d’une collision ou non. Lorsqu’une collision est détectée, alors la balle rebondit.
Pour un résultat optimal, il faudrait en fait détecter toutes les collisions et ensuite seulement appliquer le rebond qui convient. Dans le cas d’une collision unique, cela revient à ce que nous avons fait. S’il existe plusieurs collisions (pas plus de deux théoriquement), il faudrait déterminer une normale fictive, résultante des normales aux deux segments percutés, comme ci-dessous :
En pratique, ce problème
est mineur car généralement, immédiatement après avoir rebondi sur le segment
vert, la balle rebondit sur l’orange et tout se passe correctement. Mais
parfois, la nouvelle position de la balle ne touche plus le segment orange
après le rebond sur le vert, donc la balle poursuit sa course alors qu’elle
aurait du taper les deux segments.